nsq优先队列——inFlightPqueue源码分析

一、优先队列（priority queue）基本概念

在对inFlightPqueue进行分析之前，先简单介绍一下优先队列的概念。
我们都知道，队列是一种先进先出（FIFO）的数据结构。而优先队列不再遵循先入先出的原则，而是分为两种情况：
1、最大优先队列，无论入队顺序，当前最大的元素优先出队。
2、最小优先队列，无论入队顺序，当前最小的元素优先出队。

二、优先队列的实现

• 优先队列的实现常选用二叉堆，在数据结构中，优先队列一般也是指堆。

二叉堆

• 我们通常使用数组存储二叉堆，那么二叉堆在数组中又是怎么存储的呢？

用数组存储二叉堆 对于数组中的任意位置 i 的元素，其左儿子在位置 2i 上，则右儿子在 2i+1 上，父节点在 在 i/2（向下取整）上。通常从数组下标1开始存储，这样的好处在于很方便找到左右、及父节点。如果从0开始，左儿子在2i+1,右儿子在2i+2,父节点在(i-1)/2（向下取整）。

三、nsq优先队列——inFlightPqueue的实现

在nsq中实现了两个优先队列结构，都是最小堆。它们在nsq中的应用如下：

• 一是将已投递给客户端的消息加上超时时间放入优先队列，并启动ticker检查检查堆顶元素的到期时间，如果客户端收到消息及时回复FIN，会从优先队列中删除对应消息，但如果有消息到期，则会重新投递，以此保证nsq的消息最少投递一次。
• 二是用来实现延迟消息，同样是以消息的到期时间作为关键字存入优先队列，原理和上一个相同。

本文主要剖析nsq用于保证消息最少投递一次的队列inFlightPqueue。废话不多说，上代码。

package nsqd

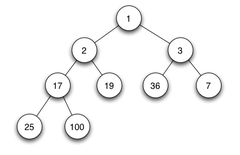
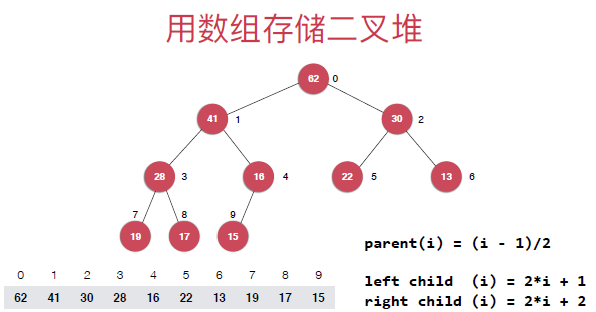
//优先队列、小顶堆
type inFlightPqueue []*Message

func newInFlightPqueue(capacity int) inFlightPqueue {
	return make(inFlightPqueue, 0, capacity)
}

//元素交换
func (pq inFlightPqueue) Swap(i, j int) {
	pq[i], pq[j] = pq[j], pq[i]
	pq[i].index = i
	pq[j].index = j
}

//向最小堆插入新值
func (pq *inFlightPqueue) Push(x *Message) {
	n := len(*pq)
	c := cap(*pq)

	//如果队列长度达到slice cap，进行扩容
	if n+1 > c {
		//cap * 2
		npq := make(inFlightPqueue, n, c*2)
		copy(npq, *pq)
		*pq = npq
	}
	//队列length + 1
	*pq = (*pq)[0 : n+1]

	//追加到堆尾
	x.index = n
	(*pq)[n] = x

	//上浮
	pq.up(n)
}

//推出堆顶元素，即最小元素
func (pq *inFlightPqueue) Pop() *Message {
	n := len(*pq)
	c := cap(*pq)
	//把堆顶元素和堆尾元素互换
	pq.Swap(0, n-1)
	//新的堆顶元素下沉重构小顶堆
	pq.down(0, n-1)
	//如果新的队列长度小于容量的一半，进行缩容（容量小于25的队列不缩容）
	if n < (c/2) && c > 25 {
		npq := make(inFlightPqueue, n, c/2)
		copy(npq, *pq)
		*pq = npq
	}
	//被置换到堆尾元素的最小元素作为返回值
	x := (*pq)[n-1]
	x.index = -1
	//队列长度-1
	*pq = (*pq)[0 : n-1]
	return x
}

// 移除指定元素
// 思路：把元素和堆尾元素交换，再重构除堆尾元素外的小顶堆
func (pq *inFlightPqueue) Remove(i int) *Message {
	n := len(*pq)
	if n-1 != i {
		pq.Swap(i, n-1)
		pq.down(i, n-1)
		pq.up(i)
	}
	x := (*pq)[n-1]
	x.index = -1
	*pq = (*pq)[0 : n-1]
	return x
}

//将入参和堆最小元素比较，小于则返回两者差值，大于则进行pop操作
func (pq *inFlightPqueue) PeekAndShift(max int64) (*Message, int64) {
	if len(*pq) == 0 {
		return nil, 0
	}

	x := (*pq)[0]
	if x.pri > max {
		return nil, x.pri - max
	}
	pq.Pop()

	return x, 0
}

//节点上浮
func (pq *inFlightPqueue) up(j int) {
	for {
		//获取父节点索引
		i := (j - 1) / 2 // parent
		//节点关键字大小比较，子更小，则上浮，否则结束循环
		if i == j || (*pq)[j].pri >= (*pq)[i].pri {
			break
		}
		pq.Swap(i, j)
		j = i
	}
}

//节点下沉
func (pq *inFlightPqueue) down(i, n int) {
	for {
		//左子节点索引
		j1 := 2*i + 1
		if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
			break
		}
		j := j1 // left child

		//左子节点和右子节点关键字值做比较，选出最小子节点
		if j2 := j1 + 1; j2 < n && (*pq)[j1].pri >= (*pq)[j2].pri {
			j = j2 // = 2*i + 2  // right child
		}
		//节点和最小子节点比较，子节点更小则进行位置交换，否则结束循环
		if (*pq)[j].pri >= (*pq)[i].pri {
			break
		}
		pq.Swap(i, j)
		i = j
	}
}